|
|
 |
TRÓJKĄT PASCALA Jednym z najbardziej interesujących układów liczbowych jest trójkąt Pascala (od nazwiska Blaise'a Pascala, sławnego francuskiego matematyka i filozofa).
|
|
Aby zbudować trójkąt, zacznij od „1” na wierzchołku, następnie kontynuuj układanie liczb poniżej w układzie trójkąta.
Każda cyfra stanowi sumę dwóch wyżej położonych liczb, np. 1 + 3 = 4.
Przekątne
Pierwsza przekątna to oczywiście same „jedynki”, następna przekątna ma liczby naturalne, trzecia przekątna utworzona została z liczb trójkątnych, tj.: kolejność stanowi wzór punktów tworzących trójkąt. Dodając kolejny wiersz z kropkami i sumując wszystkie punkty, można znaleźć następną liczbę w sekwencji
|
|
Czwarta przekątna ma liczby czworościenne:
|
|
 |
 |
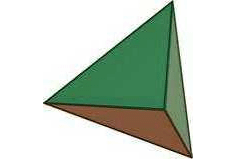
| Czworościan ma piękną i unikalną właściwość… wszystkie cztery wierzchołki są położone w takiej samej odległości od siebie. Jest to jedyna bryła Platona (platońska) niezawierająca równoległych płaszczyzn. |
|
|
Interesujące fakty:
- Posiada 4 płaszczyzny
- Każda płaszczyzna ma 3 krawędzie i stanowi trójkąt równoboczny
- Posiada 6 krawędzi
- Ma 4 wierzchołki, gdzie spotykają się 3 krawędzie
Oraz dla przypomnienia:
Powierzchnia = √3 x (długość krawędzi)²
Objętość = √2/12 x (długość krawędzi)³ Liczbę czworościenną można zrozumieć, jeżeli wyobrazimy sobie stos kul w kształcie czworościanu. Policzyć trzeba, ile kul potrzeba do zbudowania stosu o danej wysokości.
|
|
- Dla wysokości = 1 potrzebna jest tylko jedna kula.
- Dla wysokości = 2 potrzebne są 4 kule (1 na wierzchu i 3 na spodzie).
- Dla wysokości = 3 potrzeba 10 kul.
- Dla wysokości = 4 potrzeba 20 kul.
Ile potrzeba kul dla wysokości = 5? Każdą warstwę w czworościanie kul stanowią liczby trójkątne (1, 3, 6 itd.). Zarówno liczby trójkątne, jak i czworokątne znajdują się na trójkącie Pascala.
Tabela ukazuje wartości dla początkowych warstw.
|
|
n | Liczba trójkątna | Liczba czworokątna | Wysokość | Ilość kul w warstwie | Całkowita ilość kul | 1 | 1 | 1 | 2 | 3 | 4 | 3 | 6 | 10 | 4 | 10 | 20 | 5 | 15 | 35 | 6 | 21 | 56 |
|
|
Liczby parzyste i nieparzyste
Jeżeli oznaczymy oddzielnie liczby parzyste i nieparzyste, to otrzymamy układ podobny do trójkąta Sierpińskiego
|
|
Trójkąt Sierpińskiego – niekończący się układ trójkątów
|
|
Oto jak można utworzyć trójkąt Sierpińskiego:
1. zacznij od trójkąta
2. zmniejsz trójkąt o połowę i wstaw kopię w każdy z trzech rogów
3. powtórz krok 2, aby uzyskać mniejsze trójkąty, itd. w nieskończoność!
|
|
Można użyć dowolnego kształtu:
|
|
 |
 |
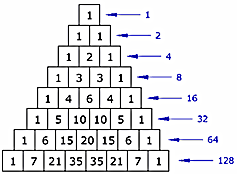
Co można zauważyć w sumach poziomych: Czy jest jakiś wzór? Niewiarygodne!
Suma podwaja się w kolejnych wierszach! |
|
|
Ciąg Fibonacciego
Ciąg można otrzymać, idąc w górę i na bok i dodając liczby, tak jak pokazano to na ilustracji… otrzymamy ciąg Fibonacciego przez dodanie do siebie dwóch poprzednich liczb.
|
|
Orły i reszki Trójkąt Pascala może pokazać wszystkie możliwe kombinacje orłów i reszek, np. można wykonać trzy rzuty monetą, ale jest tylko jedna kombinacja dająca w wyniku trzy orły (OOO), a są trzy kombinacje, które dają 2 orły i jedną reszkę (OOR, ORO, ROO), również są trzy kombinacje dające jednego orła oraz dwie reszki (ORR, ROR, RRO) oraz jedną kombinację na wszystkie trzy reszki (RRR) – stanowi to wzór „1, 3, 3, 1” w trójkącie Pascala!
|
|
Rzuty | Możliwe wyniki (w grupach) | Trójkąt Pascala | 1 | O
R | 1, 1 | 2 | OO
OR, RO
RR | 1, 2, 1 | 3 | OOO
OOR, ORO, ROO
ORR, ROR, RRO
RRR | 1, 3, 3, 1 | 4 | OOOO
OOR, OORO, OROO, ROOO
OORR, OROR, ORRO, ROOR, RORO, RROO
ORRR, RORR, RROR, RRRO
RRRR | 1, 4, 6, 4, 1 | | itd... | |
|
|
Jakie jest prawdopodobieństwo otrzymania dokładnie dwóch orłów przy 4 rzutach monetą?
Istnieje 1 + 4 + 6 + 4 + 1 = 16 (lub 4 x 4 = 16) możliwych wyników, a 6 z nich daje dokładnie dwa orły. Czyli prawdopodobieństwo wynosi 6/16 lub 37,5%. Kombinacje Trójkąt także pokazuje, jak wiele kombinacji obiektów jest możliwych.
Przykład: Mamy 16 kul. Na ile różnych sposobów można wybrać 3 z nich (pomijając, w jakim porządku się je wybiera)?
Odpowiedź: idź do rzędu 16 (górny rząd to 0), a następnie wzdłuż 3. miejsca w bok i wartość tam zamieszczona jest odpowiedzią – 560. Oto fragment rzędu 16: 1 14 91 364 ...
1 15 105 455 1365 ...
1 16 120 560 1820 4368 ... Wielomiany
Trójkąt Pascala może także wskazać współczynniki w dwumianowym rozwinięciu: |
|
Potęga | Rozszerzenia wielomianu | Trójkąt Pascala | 2 | (x+1)² = 1x² + 2x + 1 | 1, 2, 1 | 3 | (x+1)³ = 1x³ + 3x² + 3x + 1 | 1, 3, 3, 1 | 4 | (x+1)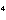 = 1x = 1x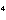 + 4x³ + 6x² + 4x +1 + 4x³ + 6x² + 4x +1 | 1, 4, 6, 4, 1 | | itd... | |
|
|
Pierwszych 15 linii
Oto rzędy od 0 do 14 w trójkącie Pascala:
|
|
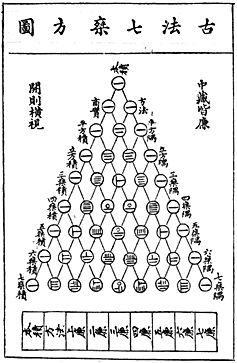
Chińczycy znali trójkąt Pascala
|
|
 |
 |
Rysunek nazywa się: „Siedem Mnożących Kwadratów”. Stanowi on stronę tytułową książki
„Chu Shi-Chieh’s” (Lustro Czterech Elementów), napisanej w roku 1303. |
|
|
 |
 |
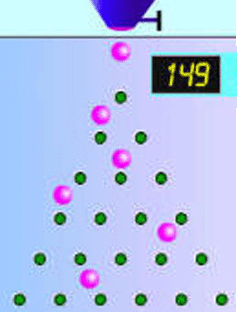
Niezwykła maszyna stworzona przez Sir Francisa Galtona oparta jest na trójkącie Pascala. Zwana jest Quincunx i składa się z kołków.
Kule opadają na pierwszy kołek, a następnie opadają na dno trójkąta, gdzie zbierają się w małych pojemnikach.
Na pierwszy rzut oka wygląda to na chaotyczny proces, ale w rzeczywistości kule zbierają się w uporządkowany stos, w kształcie tzw. standardowego rozkładu – patrz rysunek. |
|
|
|
 |
|

