|
|
 |
Fraktale Fraktal to pofragmentowany geometryczny kształt, który można podzielić na części, z których każda (przynajmniej w przybliżeniu) jest zmniejszoną rozmiarowo kopią całości. Właściwość ta nazywa się samo podobieństwo. Ogólnie mówiąc, jeżeli powiększymy jedną część, to będzie wyglądała tak samo jak większy obraz. |
|
Liść paproci jest dobrym przykładem. Fraktale opisują też inne realne obiekty jak na przykład chmury, góry, turbulencje, linie brzegowe mórz, które nie są podobne do prostych geometrycznych kształtów. |
 |
 |
|
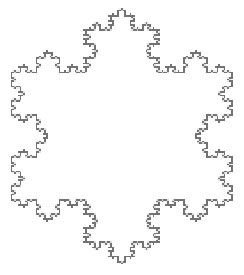 |
 |
Oto fraktal zwany płatkiem śniegu Kocha. |
|
Aby go wykonać zaczynamy od trójkąta równobocznego. |
 |
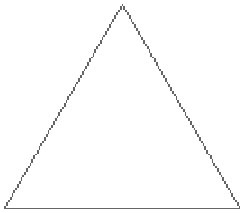 |
|
 |
 |
Zamień każdą prostą linię: |
|
Na coś co wygląda następująco: |
 |
 |
|
 |
 |
Następnie, zamień każdą prostą linię: |
|
Na coś co wygląda następująco:
I tak dalej. |
 |
 |
|
Oto jak wygląda płatek śniegu Kocha w pierwszych kilku etapach. |
|
 |
 |
Wiele innych fraktali można zbudować w ten sposób, na przykład pokazany obok trójkąt Sierpińskiego.
|
|
Oto kilka uwag matematycznych. Wyobraź sobie, że opisałeś okrąg wokół płatka śniegu Kocha. W żadnym punkcie płatek Kocha nie będzie wystawał poza linię graniczną okręgu. Zatem, płatek ma skończoną powierzchnię, gdyż jego powierzchnia jest mniejsza niż powierzchnia okręgu, która jest skończona. Jednakże, na każdym etapie budowania płatka śniegu, obwód jest mnożony przez 4/3 – zawsze się zwiększa. Tak więc, idealny płatek śniegu (przez idealny rozumiemy podążanie za nieskończoną ilością etapów konstrukcyjnych figury) ma nieskończony obwód (początkowy obwód x 4/3 x 4/3 x 4/3 x …), ale skończoną powierzchnię. Nie jest paradoks; to pop prostu fraktal. Źródło: https://home.adelphi.edu/~stemkoski/mathematrix/fractal.html |
|
|
 |
|

