|
|
 |
SYSTEM LICZBOWY STAROŻYTNYCH GREKÓW
|
|
Podczas pierwszego millenium przed narodzeniem Chrystusa w Grecji nie istniały obowiązujące normy państwowe, gdyż poszczególne wyspy greckie tworzyły oddzielne państwa. Oznacza to, że każde z nich miało swoją własną walutę, system wag i miar, a system liczbowy nieznacznie różnił się. W owych czasach liczby wykorzystywano głównie w transakcjach handlowych.
Istniały również inne systemy liczbowe zaproponowane przez różnych greckich matematyków, ale nie weszły one do powszechnego zastosowania.
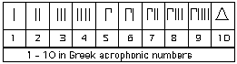
Pierwszym greckim systemem liczbowym, któremu się przyjrzymy jest system akrofoniczny, który stosowany był w pierwszym milenium przed naszą erą. „Akrofoniczny” oznacza, iż symbole liczb pochodzą od pierwszej litery nazwy liczby, tak więc symbol pochodzi od skrótu nazwy liczby. Oto symbole dla liczb 5, 10, 100, 1000, 10000.
|
|
 |
 |
Akrofoniczne 5, 10, 100, 1000, 10000. |
|
Opuściliśmy symbol dla jedności, czyli “I”, która jest naturalną prostą notacją nie pochodzącą z żadnej pierwszej litery cyfry. Dla cyfry 5 symbolem powinien być P, jeżeli nazwa brzmi Pente; jednak później nastąpiły zmiany w greckim alfabecie, a nazwa liczby pozostała bez zmian. Pierwotnie Pente brzmiało Gente.
System liczbowy był oparty o zasadę addytywności, podobnie jak liczby rzymskie. Oznacza to, że 8 jest po prostu VIII, czyli symbol 5 razem z dodanymi trzema symbolami jedności.
Oto 1 – 10 w greckim systemie akrofonicznym.
|
|
 |
 |
1-10 w greckim systemie akrofonicznym
|
|
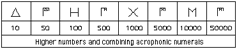
Jeżeli system dziesiętny jest również systemem addytywnym i nie występują symbole pośrednie, wtedy wiele znaków jest potrzebnych do napisania niektórych liczb. Na przykład liczba 9999 wymaga 36 symboli w takim systemie i jest to bardzo kłopotliwe. Grecki system liczbowy miał specjalny symbol dla 5. Dzięki temu skróceniu uległa ilość wymaganych znaków. Ponadto, w greckim systemie istniały pośrednie symbole dla 50, 500, 5000 oraz 50000, ale nie były to nowe symbole a raczej symbole złożone utworzone z liczby 5. Oto jak wyglądały te złożone liczby:
|
|
 |
 |
Struktura liczb akrofonicznych |
|
Należy zauważyć, że nie istniał aspekt pozycji w systemie i zero nie było potrzebne jako wskaźnik pustego miejsca. Symbol H reprezentowało 100 i nie ma tu problemu z zerami ani dziesiątkami.
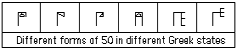
Nie był to jedyny sposób w jaki złożone symbole były tworzone. Poszczególne państewka greckie używały różne wersje symbolu tej samej liczby. Dla przykładu oto odnalezione różne warianty liczby 50. Niektóre symbole są bardzo stare; pochodzą przed 1500 r. p.n.e.
|
|
 |
 |
Różne formy liczby 50
w różnych greckich
wyspach-państewkach
|
|
Współcześnie uważamy, że liczby stanowią zbiory przedmiotów, np. liczba 2 to zbiór dwóch przedmiotów. Natomiast starożytni Grecy mieli inną ideę liczby, niż my dzisiaj. Najczęściej stosowano ten szczególny system liczbowy w rachunkach pieniężnych.
Podstawową jednostką monetarną była drachma; większa jednostka to talent równy 6000 drachm. Drachma dzieliła się na mniejszą jednostkę zwaną obolem. Jeden obol stanowił 1/6 drachmy. Obol z kolei dzielił się na 8 chalkos, czyli 1 chalkos = 1/8 obola. Należy zauważyć, iż system monetarny nie był systemem dziesiętnym, pomimo, że podstawowym systemem liczbowym był system dziesiętny, a pomocniczy system oparty był o liczbę pięć.
Poszczególne jednostki waluty były zapisywane w ten sposób, iż modyfikowano notację jednostek w liczbie.
|
|
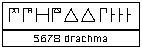
5678 drachm było zapisywane w ten sposób: |
 |
 |
|
Forma jednostek wskazywała, że mamy do czynienia z drachmami.
|
|
3807 talentów byłoby zapisane w sposób następujący: |
 |
 |
|
Występuje tutaj T ( T jak talent ).
Suma pieniędzy z drachmami i obolami wyglądała następująco:
|
|
3807 drachm i 3 obole:
|
 |
 |
|
System akrofoniczny był używany nie tylko w systemie monetarnym, ale również w systemie wag i miar. System monetarny wywodzi się ze systemu wagowego. Dowodem na to jest to, iż drachma była nazwą również jednostki wagi.
Istniał również drugi system liczbowy w starożytnej Grecji, w którym nazwy liczb pochodzą od liter alfabetu. Warto tu zauważyć, iż starożytni Grecy byli jedną z pierwszych cywilizacji, którzy używali litery alfabetu. Alfabet ten, po niewielkich zmianach, przejęli od Fenicjan, którzy go wynaleźli.
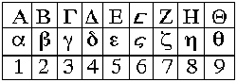
Klasyczny grecki alfabet składa się z 24 liter, używanych razem z 3 starszymi literami, które obecnie wyszły z użycia. Oto te 27 liter:
|
|
 |
 |
Alfabetyczne 1 - 9 |
|
W alfabecie są litery duże i małe. Litery stare to: digamma, koppa, i san. Pierwsze dziewięć liter stanowią symbole dla liczb 1, 2, …,9.
Proszę zauważyć, iż 6 reprezentuje przestarzała litera digamma
|
|
 |
 |
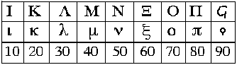
Alfabetyczne 10 - 90
|
|
Następne dziewięć liter są symbolami dla 10, 20, …., 90. Liczbę 90 reprezentuje stara litera koppa.
|
|
 |
 |
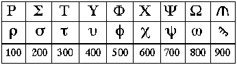
Alfabetyczne 100 - 900
|
|
Pozostałe 9 liter reprezentują liczby 100, 200, …, 900. Liczbę 900 reprezentuje stara litera san. Czasami, gdy litery te reprezentowały liczby, to aby odróżnić je od prawdziwych liter w zdaniu, nad nimi umieszczano kreskę.
Liczby były tworzone na zasadzie addytywności. Na przykład 11, 12, …., 19 były pisane w następujący sposób.
|
|
 |
 |
Alfabetyczne 11 - 19 |
|
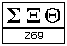
Duże liczby były budowane w podobny sposób. Na przykład 269:
|
 |
 |
|
Jest to dość kompaktowy system liczbowy, ale aby możliwe było przedstawianie liczb większych od 999 to niezbędna była jego modyfikacja. Liczby od 1000 do 9000 zostały utworzone przez dodanie indeksu górnego lub dolnego iota do symboli 1 do 9.
|
|
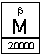
W jaki sposób Starożytni Grecy pisali liczby większe od 9999? Używali miriadę, czyli 10000. Pisano symbol M razem z mniejszymi od 9999 liczbami umieszczonymi nad nim, co oznaczało, że należy te mniejsze liczby pomnożyć przez 10000. Czyli ß umieszczona nad M reprezentowało liczbę 20000: |
|
 |
 |
Liczba 20000. |
|
 |
 |
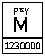
Podobnie pisane powyżej M reprezentowało 1230000: |
|
 |
 |
Liczba 1230000. |
|
Pisanie dużej liczby powyżej M sprawiało niekiedy trudności, więc w takich wypadkach liczbę tę pisano przed literą M . Przykład pochodzący z dzieł matematyka Aristarkusa:
|
|
Dla większości celów system ten był wystarczający do pisania wszystkich liczb będących w zwykłym codziennym użyciu. Liczby tak duże jak np. 71755875 rzadko występowały w życiu codziennym starożytnych Greków.
Jednak dwóch znanych greckich uczonych zaproponowało zapis liczb o bardzo dużych wartościach. Pierwszy przykład pochodzi od Apolloniusza, a drugi od Archimedesa. System, który wyjaśniliśmy powyżej działa na zasadzie mnożenia przez miriadę. Natomiast idea Apolloniusza polegała na rozszerzeniu systemu liczbowego na większe liczby dzięki podnoszeniu do potęgi miriady czyli M z symbolem α ponad nim reprezentuje 10000; M z ß ponad nad nim przedstawia M2, czyli 100000000, itd. Liczbę, którą mnożymy przez 10000, 100000000, itd. jest pisana po symbolu M, a symbol jest pisane wewnątrz liczby – jest to słowo, które najlepiej interpretować jako „plus”. Jako przykład oto w jaki sposób Apolloniusz napisałby liczbę 587571750269.
|
|
Archimedes skonstruował podobny system, nie użył jednak 10000 = 104 jako liczby podstawowej, lecz 100000000 = 108 było liczbą podstawowa. Według Archimedesa pierwszy oktet składał się z liczb do 108, natomiast drugi oktet składał się z liczb od 108 do 1016. Przy pomocy tej metody Archimedes obliczył,
że ilość ziarenek piasku, która może pomieścić się we Wszechświecie była rzędu ósmego oktetu, czyli 1064. |
|
|
 |
|

