|
|
 |
Równanie kartezjańskie: y = mx + c lub parametrycznie: x = at + b, y = ct +d |
|
Linia prosta była jedną z pierwszych badanych krzywych geometrycznych. Euklides jednak w swoich Elementach nie uważał linię prostą jako krzywą geometryczną. Po raz pierwszy ogólną definicje krzywej podał Jordan w swojej pracy "Cours d'Analysein" w 1893 roku. W przyrodzie istnieje wiele zjawisk powiązanych ze sobą w sposób liniowy. Na przykład pod wpływem siły rozciągającej pręt wydłuża się liniowo. Linia prosta miała duże znaczenie w starożytnym Egipcie, kiedy to odmierzanie ziemi odbywało się przy pomocy lin i sznurów. Herodot opisuje, iż po cofnięciu się wód wylanych przez Nil, przy pomocy napiętych lnianych lin wyznaczano ponownie granice pól uprawnych. Również linie proste wyznaczające granice budowli piramid oraz świątyń wyznaczano linami.
Proste linie w naszym otoczeniu są głównie zaprojektowane przez człowieka – na przykład ściany domów, okien, drzwi. W przyrodzie występują w wyniku działania siły działającej w jednym stałym kierunku, na przykład zboże rośnie w kierunku Słońca. Kamień spada wzdłuż linii prostej na ziemię.
W fizyce ruch jednostajny prostoliniowy występuje wtedy, gdy wszystkie siły działające na obiekt są w równowadze, na przykład pęcherzyki powietrza w wodzie unoszą się do góry ruchem prostoliniowym i ze stałą prędkością. |
|
Krzywa została po raz pierwszy zbadana przez Talbot’a. Ma cztery wierzchołki i dwa węzły.
Jeżeli krzywą Talbot’a zapiszemy równaniami parametrycznymi:
x = (1 + a sin2 t) cos t
y = (1 – a – a cos2 t) sin t
to w zależności od wartości a otrzymujemy następujące postacie krzywej:
|
|
a = 9/10 a = 1/2 a = 11/10 a = 1
|
|
 |
 |
Tarcza wojownika plemienia Zulu w kształccie krzywej Talbot'a
|
|
Parametryczne równanie kartezjańskie: x = 1/cosh(t), y = t - tanh(t)
|
|
Traktrysa jest to krzywa, dla której długość odcinka stycznej liczona od punktu styczności M do punktu przecięcia tej stycznej z daną prostą P jest wielkością stałą. PM = OA = const
|
|
Po raz pierwszy krzywą badał Claude Perrault w 1670, następnie Sir Isaac Newton (1676) oraz Huygens w 1692 roku, który stawiał zagadnienie w następujący sposób: dany jest nierozciągliwy sznurek poruszający się po linii prostej i ciągnący za sobą dowolny obiekt. Jaki jest wtedy tor ruchu obiektu? Na przykład środek tylnej osi samochodu ciągniony liną ze stałą prędkością i w stałym kierunku (początkowo prostopadle do osi samochodu). Z tego względu krzywa niekiedy nazywana jest wleczoną lub traktorią, oraz rzadko krzywą osła. Trahere po łacinie oznacza ciągnąć, wlec. Funkcja ma poziomą asymptotę, a krzywa jest symetryczna względem Oy. Krzywę badali również Leibniz, Johann Bernoulli i inni. Ewolutą (rozwinięta) traktrysy, a więc zbiorem wszystkich jej środków krzywizny c, jest krzywa łańcuchowa. Ponadto, traktrysa ma taką właściwość, iż długość stycznej od jej punktu styczności do asymptoty jest wielkością stałą.
Pole powierzchni pomiędzy traktrysą, a jej asymptotą jest wartością skończoną.
Krzywa o nazwie traktrysa znana jest od drugiej połowy XVII wieku. Uczeni zajmowali się nią w związku z poszukiwaniem odpowiedzi na pytanie: po jakiej krzywej w płaszczyźnie poziomej porusza się punkt materialny zamocowany na końcu M nici MP, stałej długości a, której koniec P przesuwa się wzdłuż prostej L.
Gdy traktrysę obrócimy wokół jej asymptoty to powstaje pseudosfera. Pseudosfera jest to powierzchnia o stałym ujemnym zakrzywieniu
(w przeciwieństwie do sfery, która ma stałą dodatnią powierzchnię). Została ona wykorzystana przez Beltrami’ego (1868) w swojej szczegółowej pracy dotyczącej interpretacji geometrii nieeuklidesowej Łobaczewskiego. |
|
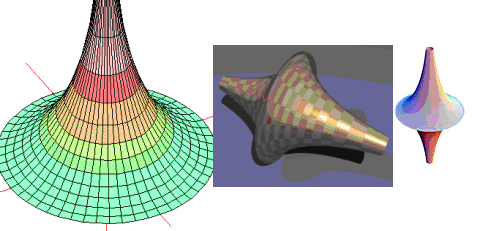 |
Powierzchnia powstała w wyniku obrotu wokół asymptoty.
|
|
Oznaczmy przez R maksymalną odległość od osi punktów powierzchni pseudosfery (promień pseudosfery).
Pole powierzchni S i objętość V pseudosfery wynoszą odpowiednio:
S = 4 R2; V = 4/3 R2; V = 4/3 R3 R3 W 1927 roku P.G.A.H. Voigt opatentował róg/trąbkę w kształcie traktrysy, której konstrukcja oparta była na założeniu, iż fala dźwiękowa poruszająca się wewnątrz rogu ma powierzchnię sferyczną o stałym promieniu. Pomysł miał na celu zminimalizowanie zniekształceń dźwięku spowodowanych wewnętrznymi odbiciami zwrotnymi fal dźwiękowych.
|
|
Róg Gabriela (lub trąbka Torricelliego) – bryła geometryczna, opisana przez Evangelistę Torricelliego, o nieskończonej powierzchni zewnętrznej, ale skończonej objętości. Nazwą nawiązuje do archanioła Gabriela, który ogłosi Sąd Ostateczny zadęciem w róg.
|
|
DELTOIDA, CZYLI HIPOCYKLOIDA O TRZECH OSTRZACH
|
|
Równanie kartezjańskie: (x2 + 12ax + 9a2)2 = 4a(2x + 3a)3 lub parametrycznie: x = a(2cos(t) + cos(2t)), y = a(2sin(t) - sin(2t))
Hipocykloida to linia, jaką opisuje ustalony punkt okręgu toczącego się bez poślizgu wewnątrz okręgu o większym promieniu. Jeżeli stosunek promienia R dużego okręgu do promienia r małego okręgu wynosi 3, to otrzymujemy deltoidę. R/r = 3.
|
|
Deltoida i jego styczne
U dołu po lewej - ewoluta utworzona przez obwiednię normalnych/prostopadłych
Po prawej - okręgi styczne do deltoidy i ich środki
|
|
Podera (krzywa spodkowa) deltoidy ze względu na ostrze, wierzchołek, lub środek stanowią krzywe w kształcie liścia (folium) z odpowiednio jedną, dwoma lub trzema pętlami (róża z trzema płatkami).
|
|
Trzy podery ( krzywe spodkowe ) deltoidy to:
Punkt podery | Podera / krzywa spodkowa | Ostrze krzywej | pojedynczy liść | Wierzchołek | podwójny liść | Środek | trójliść |
|
|
KRZYWA TRZECIEGO STOPNIA TSCHIRNHAUS'A
|
|
Równanie kartezjańskie: 3a y2 = x(x-a)2;
Równanie biegunowe: r = cos-3 ? ?
|
|
Krzywa była badana przez Tschirnhaus’a, de L’Hopital’a oraz Catalan’a. Nosi również nazwę krzywa trzeciego stopnia de L’Hopitala lub krzywa trójdzielna Catalana. Ehrenfried Walter von Tschirnhaus (1651 – 1708) był niemieckim matematykiem oraz wynalazcą europejskiej porcelany, tzw. miśnieńskiej. Urodził się jako siódme dziecko u Saskiego urzędnika sądowego. Pobierał prywatnie lekcje matematyki będąc jeszcze w szkole podstawowej. Studiował matematykę i filozofię na Uniwersytecie w Leiden. Pracował nad rozwiązaniami równań oraz badał obwiednie promieni świetlnych emitowanych z punktowego źródła i po odbiciu od powierzchni o kształcie danej krzywej. Istnieje spirala sinusoidalna nazwana na jego cześć. Jego marzeniem było uzyskanie płatnej posady w Académie Royale des Sciences w Paryżu. Uzyskał tę posadę w 1682 r., lecz bez stałej pensji. Eksperymentował nad uzyskaniem porcelany z mieszaniny gliny i łatwo topliwej skały. W 1680 r. fabryka w Meissen rozpoczęła produkcję porcelany wg jego receptury. Porcelana ta była nazywana "białym złotem", a wartość była porównywalna ze złotem. Mimo tego, że Chińczycy wynaleźli porcelanę w VII w. n.e., to właśnie Tschirnhaus odkrył jej recepturę w Europie, 1000 lat później.
|
|
Ehrenfried Walther von Tschirnhaus Forma wtórna krzywej |
|
Równanie kartezjańskie: y(x2 + a2) = a3 lub parametrycznie: x = at, y = a/(1 + t2)
|
|
Krzywą niniejszą opisała matematyczka z Włoch Maria Gaetana Agnesi (1718-1799) w 1748 roku w swojej pracy "Istituzioni Analitich" (ad uso della gioventu italiana). Krzywa niekiedy nazywana jest też krzywą sześcienną d’Agnesienne.
Wcześniej krzywą badał Fermat (1666) oraz Guido Grandi w 1703 roku.
Krzywa leży między y = 0 oraz y = a. Punkt przegięcia wynosi y = 3a/4. Linia y = 0 jest asymptotą krzywej.
|
|
Krzywe równoległe do krzywej d’Agnesienne.
|
|
Nazwa krzywej - Wiedźma z Agnesi – ma ciekawą historię. Maria Agnesi początkowo nazwała krzywę versoria, co oznacza: „lina ciągnąca żagiel”. Versoria stała się z upływem czasu włoskim słowem la versiera, co oznacza „swobodnie poruszający się”. Lecz tłumacz książki John Colson źle przetłumaczył powyższe słowo, mianowicie na l’aversiera, co oznacza po włosku niewiastę przeciwną Bogu. Dlatego dzisiaj krzywa zwana jest versierą lub wiedźmą z Agnesi.
|
|
Prostopadłe oraz ewoluta Wiedźmy z Agnesi
|
|
Okręgi styczne do Wiedźmy z Agnesi
|
|
Konchoidy Wiedźmy z Agnesi
|
|
Szczególnym przypadkiem jest krzywa rezonansowa. Rezonans występuje wtedy, gdy drgania zewnętrzne o wartości częstotliwości zbliżonej do pewnej częstotliwości rezonansowej, wymuszane są względem danego układu. Przykładem jest monochromatyczne fale świetlne padające na atom. Natężenie promieniowania emitowane w następstwie przez atom posiada formę krzywej rezonansowej i jest funkcją różnicy pomiędzy częstotliwością zewnętrzną a rezonansową. Fala świetlna ma formę sinusoidy.
Krzywa niniejsza jest również funkcją gęstości prawdopodobieństwa i nazywa się rozkładem Cauchy’ego. Całką funkcji jest arcus tangensem. |
|
|
 |
|

